Since last week, Marc Henneaux has been giving a series of lectures on the Asymptotic Structure of Gravity and Gauge Theories. For those who do not know him, he is a prominent Belgian physicist who has contributed significantly to the development of Theoretical Physics. Henneaux is also a Member of the Royal Academy of Belgium and his work is devoted to the study of the algebraic structure of gauge theories, asymptotic symmetries, boundary conditions and Hamiltonian methods. He is known for having shown, alongside Brown, that the asymptotic symmetry algebra of 2+1 dimensional gravity with a negative cosmological constant is actually a direct sum of two Virasoro algebras. Notably, Max Bañados, a Chilean renowned physicist, is attending the lectures these days. There have been too many points in the lectures to describe all of them here. However, I am highlighting some of the relevant key points.
Studying the asymptotic structure of gravity is a very interesting task motivated mainly by the emergence at spatial infinity of the Bondi-van der Burg–Metzner–Sachs (BMS) symmetry, originally discovered at null infinity. However, to delve into this advanced topic it is necessary to understand first some basic concepts. For this reason, Henneaux started his lectures last week on Monday by reviewing the action principle in Hamiltonian formalism and taking into account constraint terms and boundary terms. He then defined symmetry as a transformation that makes the Lagrangian vary by a total derivative. The next tools that Henneaux nicely presented are the symplectic structure, the Lie derivative along a vector field in phase space and the internal contraction.
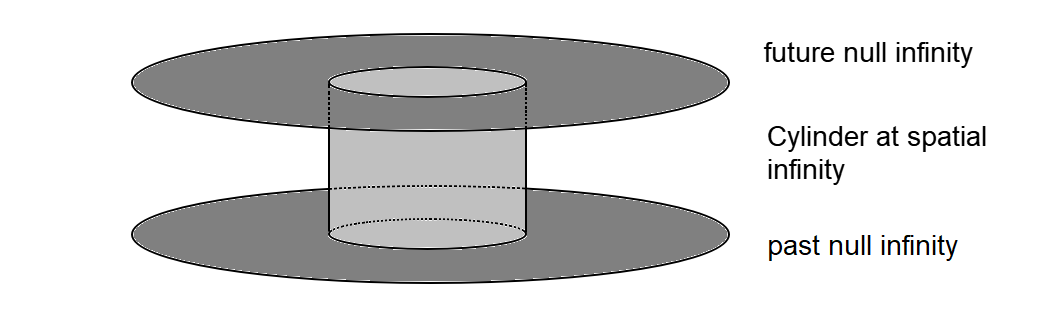
On Wednesday, Henneaux applied all the ideas and concepts presented to the case of Electromagnetism. Then, he delved into the question of connecting null infinity with spatial infinity and showed a Penrose diagram of Minkowski space. In the case of electromagnetism, we assume some behaviour of the electromagnetic field at future null infinity and another behaviour at past null infinity and we need to understand better spatial infinity if we want to see how these things connect. It is even simpler to work with a scalar field to deal with this problem. An interesting aspect was the representation of spatial infinity as a cylinder in Friedrich coordinates.
Yesterday, Henneaux started to talk about gravity in 3+1 dimensions and the BMS group. First, he reviewed the original derivation using the Bondi coordinates. He wrote out the more general asymptotically flat metric. This is like having the gravitational field over a Minkowski background. Imposing appropriate asymptotic boundary conditions one can ask For which diffeomorphisms does the transformed metric fulfil the above boundary conditions? Answering that question reveals a group (the BMS group) of asymptotic symmetries parametrized by the angular coordinates of the metric. In terms of spherical harmonics, one can see that l=0 corresponds to time translations while l=1, to space translations. A general spherical harmonic (arbitrary l) corresponds to a transformation named supertranslation. Henneaux then started to explain the Hamiltonian formalism applied to gravity with the aim of obtaining again the BMS group, but this time at the spatial infinity.
Tomorrow is the last lecture and I guess Henneaux will talk about the supertranslation ambiguity in the angular momentum and if there is enough time, he may also touch upon the subject of supergravity.
Marc Henneaux. Image from a recorded lecture available here.