Since the proposal of Celestial Holography, an idea that promises to provide a new approach to quantum gravity in a four-dimensional asymptotically flat spacetime, remarkable progress has been made. However, the original proposed dictionary causes massless two-point correlators to take the following delta-distribution like behavior
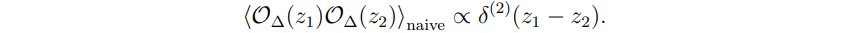
rather than the expected power-law
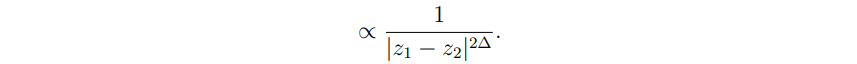
Furthermore, this behavior clashes with the operator product expansion (OPE). Recently, Hideo Furugori, Naoki Ogawa, Sotaro Sugishita and Takahiro Waki proposed a breathtaking solution in their relatively new paper:
Celestial two-point functions and rectified dictionary
Celestial holography propounds a duality between scattering in an asymptotically flat spacetime and a conformal field theory on the celestial sphere at null infinity. The main objects of study are the so-called celestial amplitudes, which recast the scattering matrix into a basis of boost (rather than energy) eigenstates. They transform like conformal correlators living on such a sphere. The theory built upon these correlators is what we call celestial conformal field theory (CCFT). Furugori and collaborators propose this rectified dictionary for massless scalars
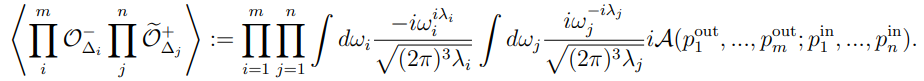
The key difference from the standard one is that they claimed that the operators corresponding to the incoming particles are the shadow-transformed operators
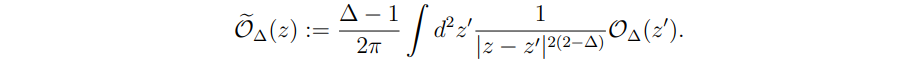
We thus have a map between scattering amplitudes in the asymptotically Minkowski background and correlators on the celestial sphere. These correlators are sometimes called celestial correlators. The authors verified that, using this dictionary, the two-point correlators of (non-shadow) operators take the conventional form in CFT, namely the power law.
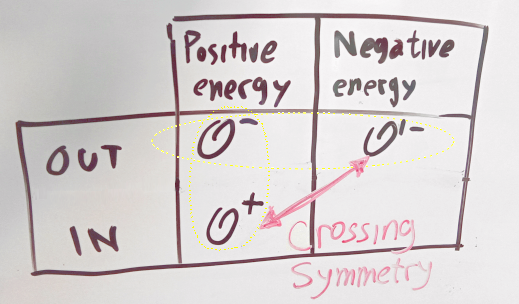
Next, they considered the celestial dictionary for massive scalars, which is the same as the naive one, up to suitable factors, and show that it is smoothly connected to the one for massless scalars – that is to say, we get the celestial dictionary for massless scalars if we take the massless limit of the one for massive scalars. Another stunning aspect is that crossing symmetry for scattering amplitudes, which relates amplitudes involving an incoming positive energy particle to ones involving an outgoing negative energy particle, has a quite natural interpretation in the CCFT. The dictionary can be rewritten treating all outgoing particles on an equal footing regardless of whether they have positive or negative energy. Then, by comparison, a relation between operators for particles with outgoing negative energy and operators for particles with incoming positive energy can be established.
In addition, they went on the validity of their dictionary using the OPE and thus ensuring the consistency of it. The three-point correlator can be schematically written as
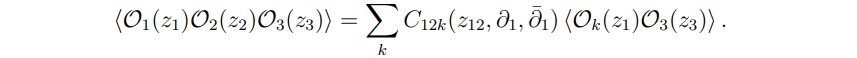
This corroborates that the three-point correlator is consistent with the two-point function power-law behavior. They subsequently considered the concrete example of a tree level scattering amplitude for two incoming massless particles and one outgoing massive particle and verified that the corresponding celestial three-point correlator behavior does not give rise to any inconsistency. In the case of the four-point correlator, they also commented that the OPE gives the expected result
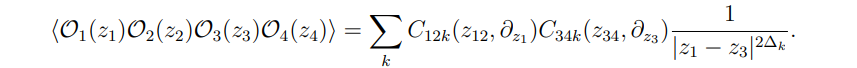
Note that it's been almost seven years from the naive celestial dictionary. I believe that this new dictionary will prompt a significant reassessment of some features of CCFT, including OPEs and the conformal block decomposition.