I recently provided an overview of Strings 2023. As I wrote then, Andrew Strominger was the first speaker of the Monday morning session. As a blackboard aficionado, Strominger didn't use any
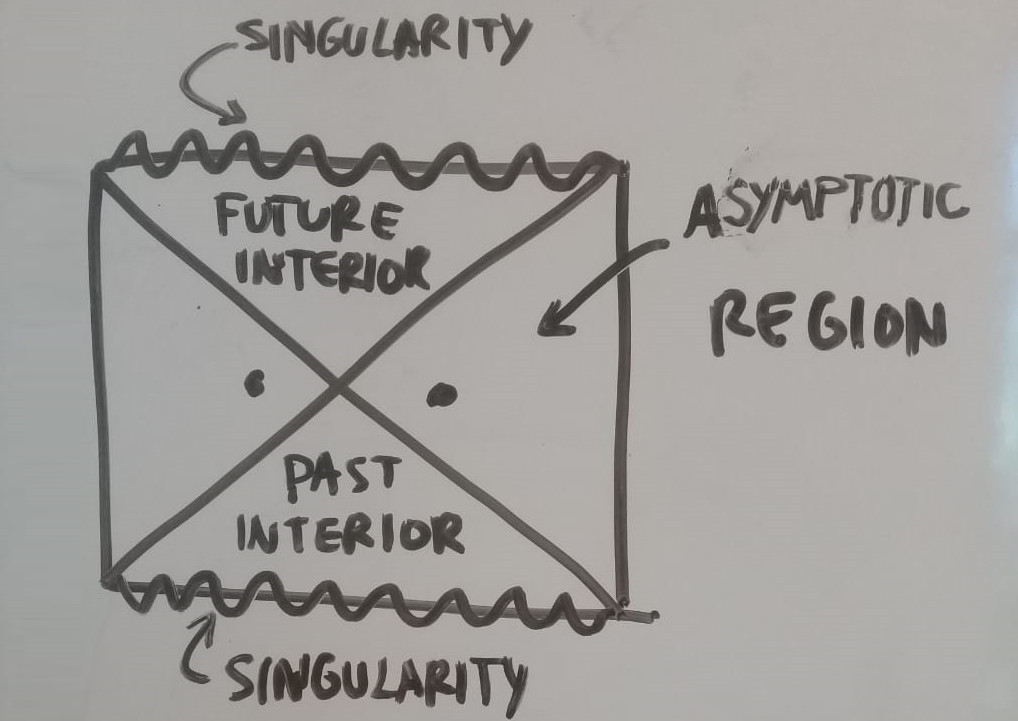
presentation slides. He began with a few words about ER = EPR. The simplest and best-understood example is in Schwarzschild Anti-de Sitter (AdS). Its Penrose diagram displays two asymptotic regions and two interiors. There are Einstein-Podolsky-Rosen correlations between quanta in different asymptotic regions. At the same time, we get the Einstein-Rosen bridge connecting the two black holes and this is the origin of the ER = EPR slogan. So spacetime itself is built up of the quantum entanglement and that
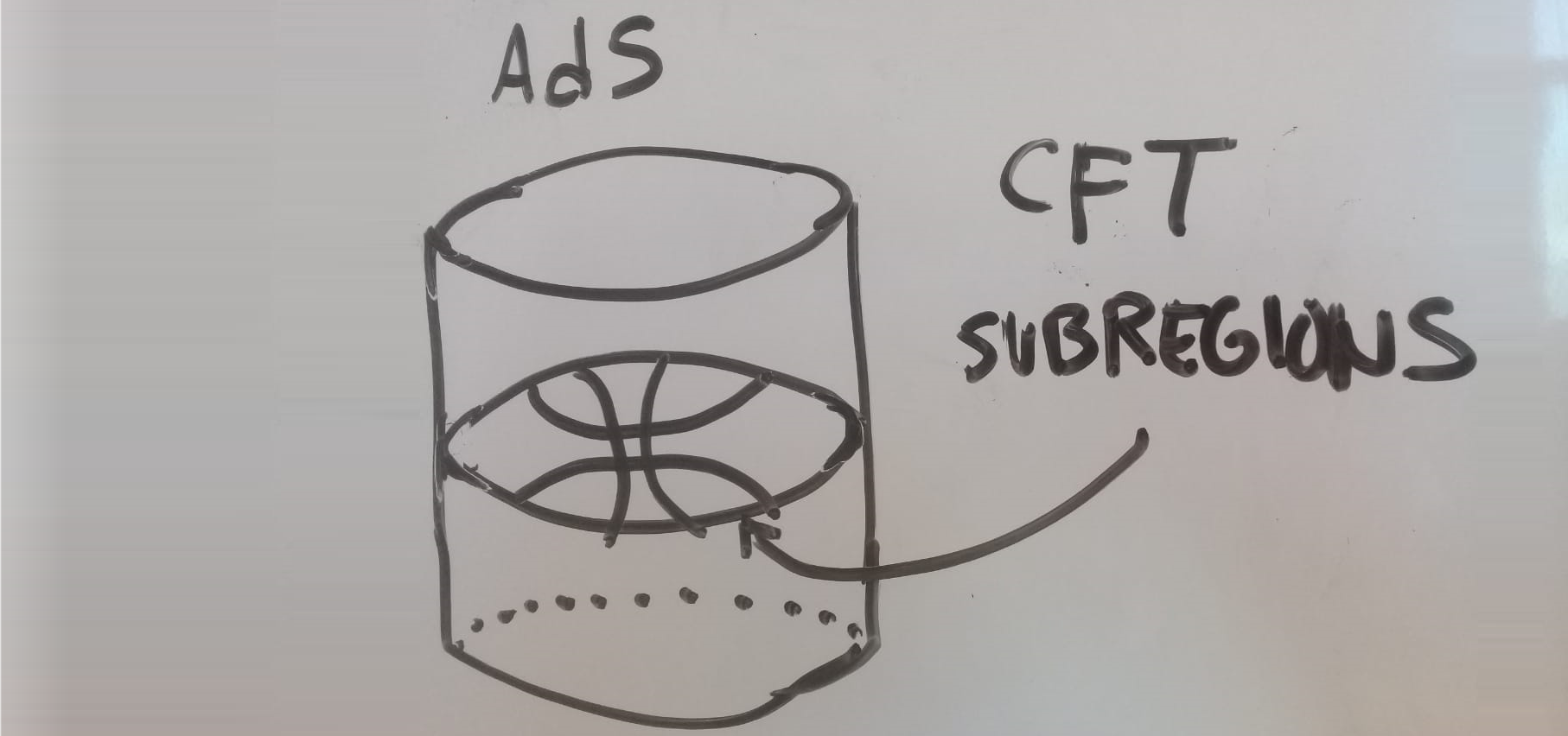
also can be seen with just usual AdS/Conformal Field Theory (CFT) by leveraging some deep concepts of quantum information theory. In this way, one can see that the bulk spacetime is built up of the quantum entanglement between CFT subregions.
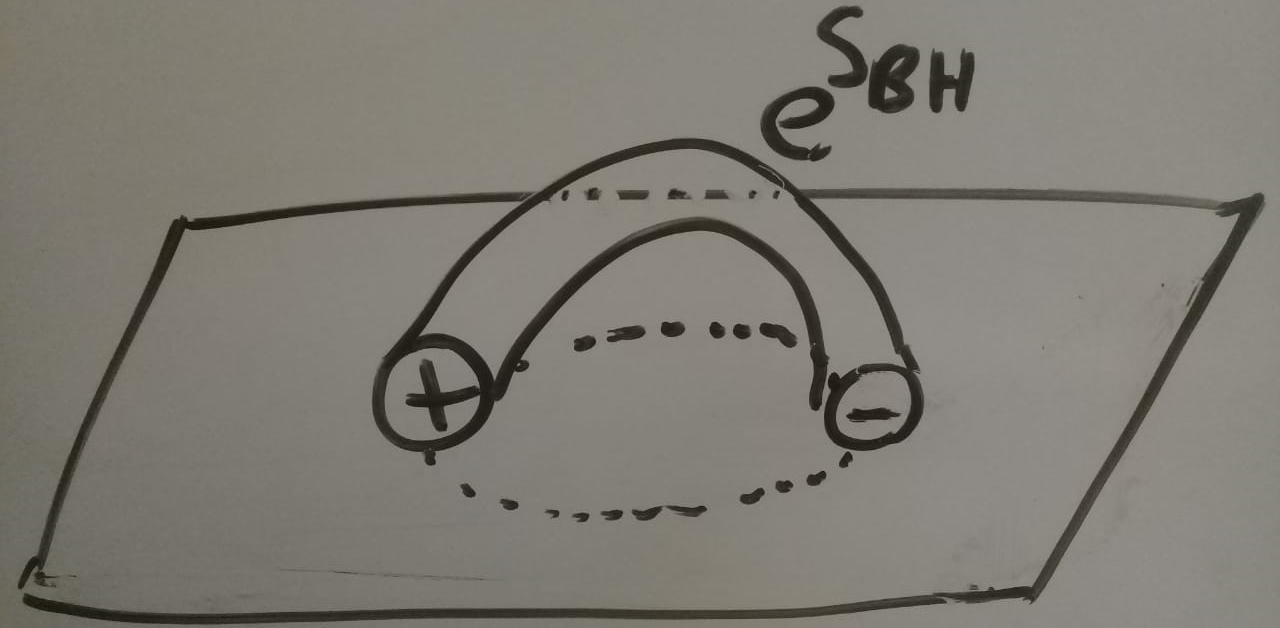
Another example, that doesn't involve AdS, is the pair production of magnetic monopoles in a magnetic field. If you make them smaller and smaller, suddenly each monopole drops inside a horizon and the instanton that creates them has a
wormhole connecting them. At the same time, the instanton action discontinuously changes by
There are two classes of quasinormal modes, labelled by plus or minus:
patch time.
Then he asserted that it is possible to construct a different class of modes, better suited for his purpose, by taking a judicious linear combination which vanishes in half the spacetime.
These new modes
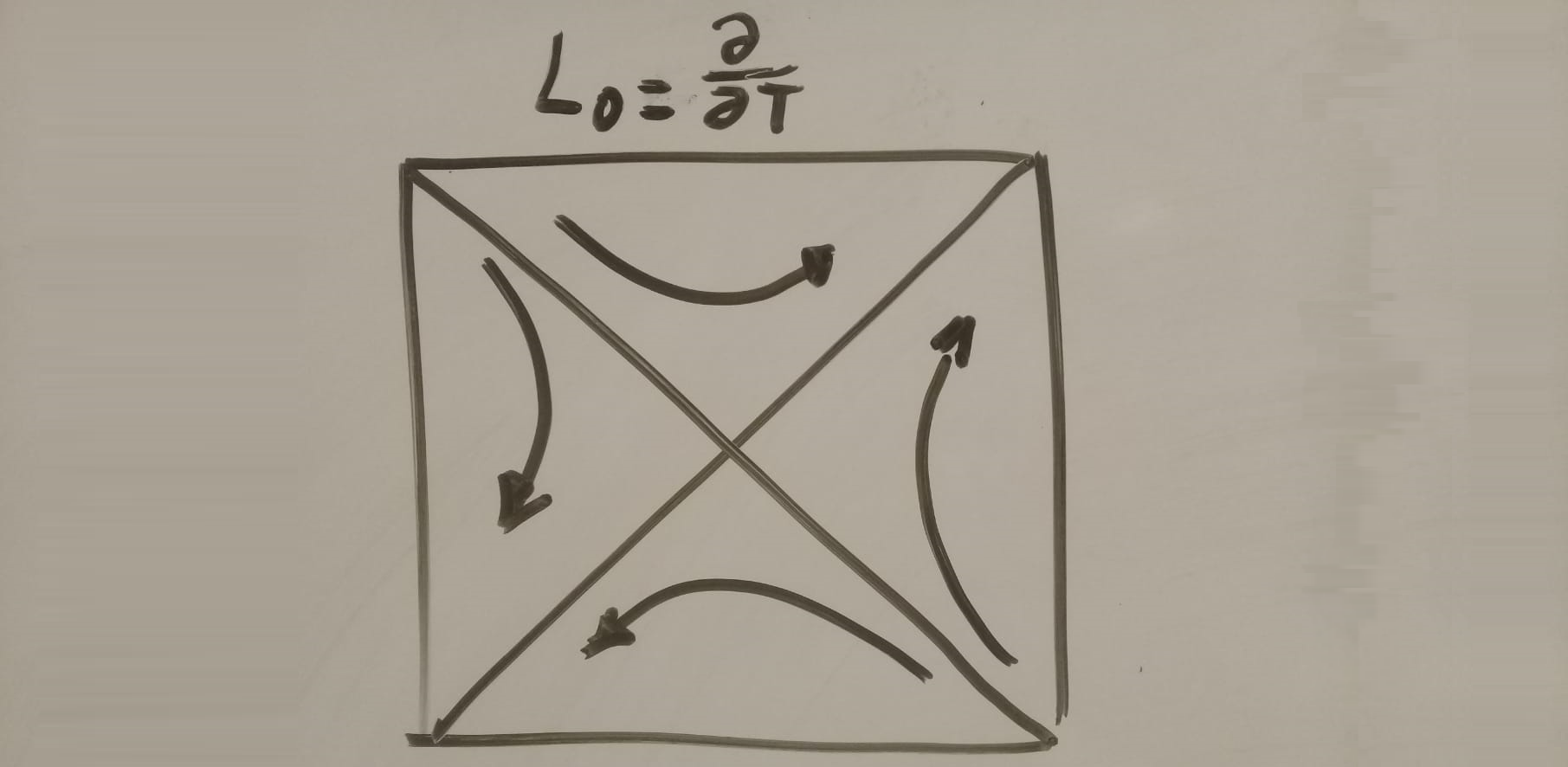
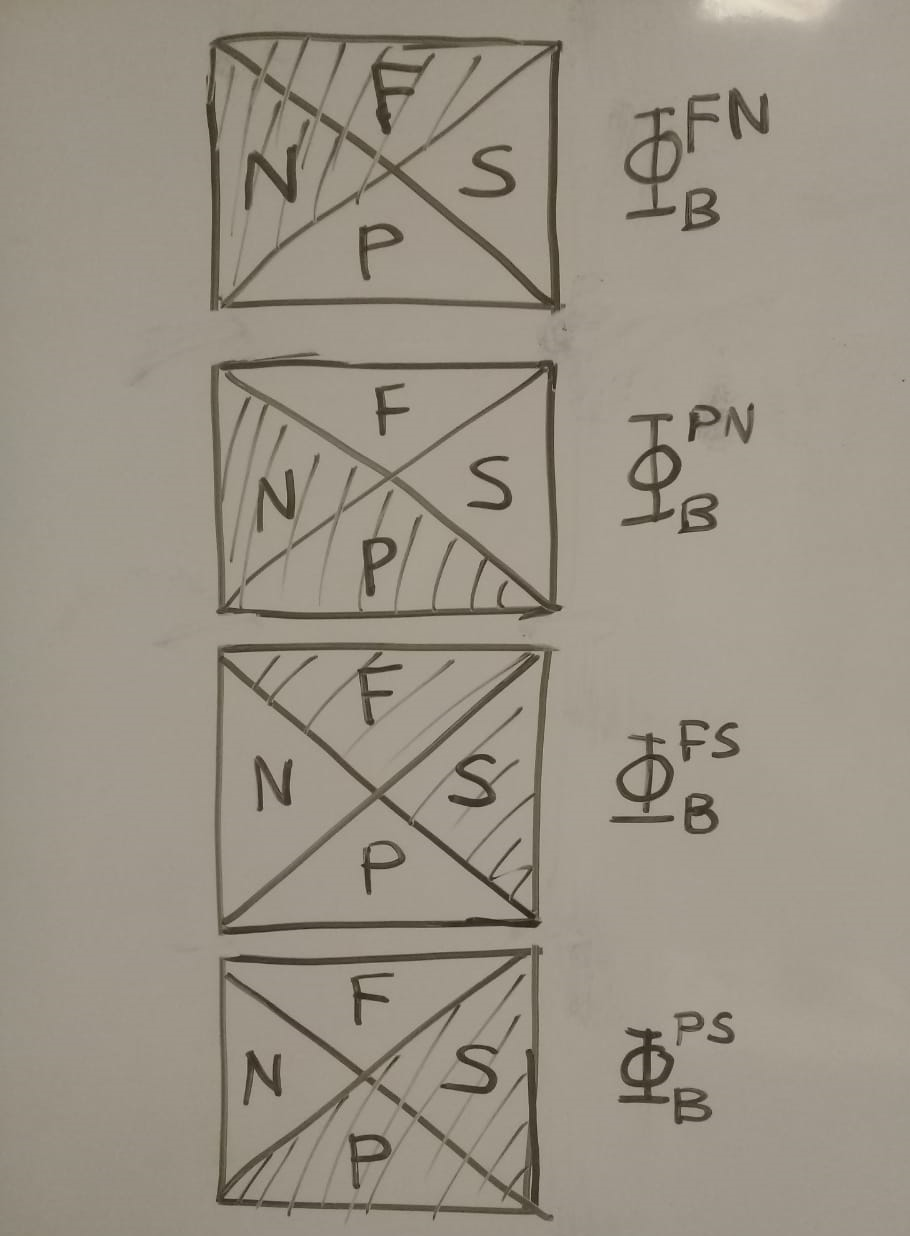
-Sbh (here Sbh is the black hole entropy) giving a factor of exp(Sbh) in the semiclassical production rate which tells you that there must be a quantum correlation between the black holes, so they are created in a pure state. After that introduction, he went on to elaborate on the de Sitter (dS) case and considered a massive scalar on it. It's important to go into the quasinormal mode basis for the scalar field. ΦQN±. They depend on h±, a conformal weight under the conformal group SO(4,1). He worked in the range where h± is real and not integer. There are also anti-quasinormal modes: ΦAQN±. Quasinormal modes and anti-quasinormal modes are eigenstates of L0 which is the derivative with respect to static ΦFNB, ΦPNB, ΦFSB, ΦPSB, form a complete basis; here F, P, N, and S stand for Future region, Past region, Northern static patch and Southern static patch respectively, in the typical Penrose diagram of dS, B is a multi-index which indicates all the descendants and each of these modes has support in its respective shaded region.
Then he worked out the commutators and the bulk reconstruction formula.
He skipped the details and wrote out the final result which was that the Euclidean vacuum |0E⟩ can be expressed as a thermofield double in the tensor product of the dual CFT3 Hilbert space. Since the isometry group of dS4 is SO(4,1) and it acts like the conformal group on the 3-spheres (S3) at the future null infinity, the dual theory should be a CFT on S3.
Moreover, the bulk Hilbert space of global dS4 is isomorphic to the tensor product of two copies of the CFT3 Hilbert space:
H global dS4 ≃ H CFT3 ⊗ H CFT3.Tr |0E⟩⟨0E| = exp(-2πi L0).
This outcome led him to suggest that the static patch partition function is dual to the CFT3 partition function at a temperature of 1/(2πi).
This seems some progress on solving the question of what counts the de Sitter entropy.
Finally, he ventured that the same idea might be applied to Celestial Holography where the Rindler wedges would give rise to the Past and the Future wedges.
Edward Frenkel began the Tuesday morning session with a Challenge Talk motivated by the old notes on quantum integrable models of a famous physicist with the plan to explain later the modern perspective, linking them to dualities. This physicist was Feynman who expected that the methods employed in solving quantum integrable models could be useful in the study of realistic models such as QCD. Frenkel introduced the Gaudin model and how the Bethe Ansatz is applicable. He sketched the Langlands correspondence along with an explanation of its formulation in three different domains. Mathematicians have greatly benefited from string theory and the explanation of S-duality of certain N = 4 4d SYM theories in terms of string theory is an example of that. Physicists interested in categories, A-branes, B-branes, etc., eventually found a way to link the Langlands correspondence to S-duality. Hence, this serves as an explanation for the Langlands correspondence. On the other hand, in mathematics we don't have an explanation yet, it is a miracle in the words of Frenkel. The main point of the talk was that the modern version of Bethe Ansatz is no longer about finding explicit formulas for eigenvectors. What is behind Bethe Ansatz is always a duality. Therefore, our challenge is to determine what this duality is. The Gaudin model case is not an isolated example, there are many others where a similar pattern holds. In most of them, we actually don't know what is the string duality. He challenged the audience to try to embed quantum field theory dualities in string theory. Frenkel concluded with open problems/questions such as Is there any string theory explanation for the affine Gaudin models’ Langlands duality? Are there applications of “Bethe Ansatz” to realistic theories like QCD? If you find this subject interesting, don't hesitate to download the slides from here.
Ashoke Sen revisited logarithmic corrections to supersymmetric black hole entropy.
He opted to begin by explaining basic things like the Bekenstein-Hawking entropy and its scaling property. From the general structure of the entropy (considering corrections due to stringy effects and quantum effects), he focused on the logarithmic correction. Sen then reviewed the general procedure for computing this correction, which involves performing a path integral over all fields satisfying the same boundary conditions as the black hole. This yields the partition function, from which the entropy can be derived using statistical mechanics rules. He outlined known results for supersymmetric black holes addressing the subtleties like the near horizon approximation and if the resulting partition function is in the microcanonical ensemble or grand canonical ensemble. He then stated their goal, which is to reproduce the known results by using the supersymmetric index introduced by Iliesiu, Kologlu and Turiaci. Before delving into black holes, he dedicated two slides reviewing what the supersymmetric index is and the key fact that it counts the degeneracy of supersymmetric ground states. This means that the gravitational path integral, with a suitable insertion, can be regarded as some appropriate integral of the supersymmetric index. By carefully considering the zero modes contribution, he obtained that the logarithmic correction to the supersymmetric index, computed from the near horizon geometry and the full geometry both give the same result. He expressed his hope that this formalism may be better suited for exact computations of the supersymmetric index (via localization for example). Regarding the question of asymptotically AdS cases, Sen clarified that the scaling now doesn't quite work the way he described, as the AdS radius also needs to be scaled. Therefore, the arguments presented in his talk don't directly apply to these cases. So, you are to study black holes propagating in a fixed theory in order to keep the AdS radius fixed, unless we are looking for logarithmic corrections involving the AdS radius.
Another interesting Challenge Talk was given by John Preskill on Thursday. After performing a brief rendition of the Maldacena song
You start with the brane
and the brane is BPS.
Then you go near the brane
and the space is AdS.
Who knows what it means?
I don’t, I confess.
Ehhhh! Maldacena!
he started to imagine what he might have said at Strings 1998 if he had been invited to talk. Preskill said that he would have probably been eager to discuss the developments in entanglement theory, computational complexity and the principles of error correction, concepts that are now part of the standard parlance of people in the "It from Qubit" collaboration. He pointed out that the assertion that spacetime emerges from entanglement has become like a mantra. Upon musing on their fruitful connections to quantum gravity such as the entanglement-wormhole correspondence, he proceeded to discuss what is currently happening in quantum information. Experimental teams are expected to make significant progress allowing for highly entangled systems to be used as measurement probes, enhancing our sensitivity to weak signals. Machine learning techniques may be required to extract useful signals from this noisy data. The concept of classical shadows of quantum states has been under development for the past few years. This method allows us, by learning properties of quantum states from feasible measurements, to predict various properties of a quantum state with a high level of accuracy. A nice feature of this procedure is that we don't need to know the observables we want to predict at the time of measurement: measure first and ask questions later. In fact, many applications of classical shadows have involved re-analyzing data from quantum experiments originally collected for a different purpose. Finally, Preskill highlighted the potential of using machine learning to advance our knowledge of physics by mentioning two results: the efficient prediction of local properties of ground states of gapped local Hamiltonians in a smoothly parametrized family and the efficient classification of quantum phases of matter. He also suggested that as quantum technology advances, we might be able to learn more about quantum gravity by doing experiments with highly complex strongly chaotic quantum systems.
On Friday, Edward Witten talked about a background independent algebra in quantum gravity.
He pointed out that the inclusion of gravity presents three significant problems when trying to associate an algebra of observables to any open set as is done in ordinary quantum field theory.
Firstly, the fluctuation of spacetime makes it difficult to accurately describe regions.
A deeper problem arises by noting that, in the absence of gravity, the association of algebra with a region depends solely on the region itself, regardless of the state of quantum fields. In gravity, contrastingly, it is unclear how this association would work since the spacetime is part of what the fields determine. Hence, the algebra should be defined independently of any particular spacetime configuration. This is referred to as Background Independence.
The third problem pertains to the meaning of the algebra. In ordinary quantum field theory, an observer can probe a system at will but only in a specified region, so it makes sense to associate an algebra to that region. However, in the context of a closed universe or cosmological models, there is no one who can probe the system from outside. Therefore, the algebra only has operational meaning if it describes the operators accessible to an observer.
In order to clarify what the algebra of operators accessible to an observer is, Witten defined an observer as a timelike worldline along which the observer can measure the quantum fields.
The algebra of operators along a timelike worldline makes sense even in the presence of gravity, so it is a reasonable substitute for what we usually consider in the absence of gravity
(an algebra of operators in a certain open set) and seems to make more sense when gravity is included.
He then focused the discussion on rethinking and considering the same construction as in the CLPW paper (which assumed an observer in de Sitter space) with the motivation of wanting background independence, rather than the symmetries of dS space.
In the absence of gravity, the observer can measure various quantities (such as scalar fields or electromagnetic fields) along its worldline which is parametrized by the proper time.
Nevertheless, in the presence of gravity, this becomes a subtle issue since the same worldline can be embedded in different ways differing by constant shifts of the proper time.
Therefore, Witten elaborated, this requires the introduction of the observer’s degrees of freedom and to define the proper time relative to some kind of clock carried by the observer.
Considering a minimal model where the observer has a Hamiltonian
m+q, he explained that allowed operators should commute with the observer's Hamiltonian plus any gravitational constraint operator that generates a shift along the worldline. The allowed operators generate an algebra which is defined as the observer algebra.
Witten emphasized the importance of interpreting this algebra as an operator product algebra rather than an algebra of Hilbert space operators in order to get background independence.
He sketched afterwards some aspects such as the characterization of the observer algebra by the universal short distance or 1/q expansion of operator products and the definition of a state of the observer algebra as a linear functional that obeys certain conditions.
In the special case of an empty dS space, Witten mentioned that there is a Penrose diagram that represents the region where the Observer can see an influence called a static patch. The generator that advances the proper time of the observer can be used as the constraint operator. In the absence of gravity, there is a notable state which has thermal correlation functions at the dS temperature.
These correlation functions have two key properties: time translation symmetry and the KMS condition.
Using a state, denoted by Ψmax, in which the observer energy has a thermal distribution at the dS temperature, one can show that they go over to properties in the presence of gravity, with the KMS condition simplifying. He then discussed the concept of density matrix. The density matrix of the state Ψmax is found to be 1, meaning it is a maximally mixed state and by using the von Neumann entropy, it is clear that it has maximum possible entropy. This provides a definition of entropy for dS space, which agrees with the usual definition of the generalized entropy up to an additive constant independent of the state.
Witten then delved into the speculative hypothesis that ΨHH, the no-boundary state with an observer, is universal allowing us to give a general definition of the entropy of an arbitrary state of the observer in any spacetime using the relative entropy concept. He concluded by considering a theory with many dS vacua (each one with a different Hilbert space) and showing that his definition gives the standard answer up to the universal additive constant −log Z in this case. This constant is universal in the sense that it is independent of the spacetime. Although Witten did not explicitly mention the nature of Z, I believe it corresponds to the no-boundary partition function. Therefore, we should have Z = ⟨ΨHH|ΨHH⟩.
I acknowledge that there may be certain aspects that are unclear in these summaries. Please feel free to provide comments, and I will gladly provide clarification. If necessary, I can also write separate posts to address specific topics.
On the temperature of the CFT3 dual to dS
Strominger's talk was based on his research paper titled "Cosmic ER=EPR in dS/CFT" (abstract, pdf), co-authored with Jordan Cotler. Once I read the paper, I realized there should be a missing negative sign somewhere. If you substitutei L0 = Hstatic into the expression rho = exp(2 π i L0), you will obtain rho = exp(2 π Hstatic), which differs from equation (4.5).
It should be noted that Strominger, during his talk, traced the Euclidean vacuum over the north while in the paper he did a southern trace. After reviewing the rest of the manuscript, I was pretty sure that it is just a matter of choice if one takes the southern trace or the northern trace. However, I was wondering about the temperature of the boundary CFT3, T = -1/(2πi), reported in the paper. So, I decided to write to Strominger to bring this issue to his attention. Jordan Cotler responded by thanking me and confirmed that indeed, either choice (north or south) is fine and, with the signs corrected, they actually have T = 1/(2π i), so the sign does not switch upon tracing out north instead of south. A new version of the paper (abstract, pdf) was uploaded shortly thereafter, which included the corrected expression rho = exp(-2 π i L0). It is always satisfying to see a mistake corrected and acknowledged in this manner.